第一章 线性方程组解法
- 代数学起源于解方程(代数方程)
- 一元一次、一元二次、一元三次、一元四次都有求根公式(通过系数进行有限次加、减、乘、除、乘方、开方得到解),一元五次以上方程就不再有求根公式了(近世代数)
- 二元一次方程组、三元一次方程组、……、n元一次方程组(线性代数研究对象)
- 高等代数——线性代数+多项式理论
1. 线性方程组的同解变形、线性组合、初等变换、消去法
- 例1

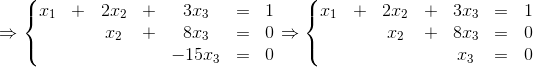

- 同解变形:用3种同解变形必可化方程组为阶梯型
- 交换两个方程位置
- 用非0的数c乘某个方程两边
- 用某个方程的k倍加到另一个方程
- 线性组合:设
 是一些方程,称
是一些方程,称 为
为 的一个线性组合。(由
的一个线性组合。(由 组成的方程组与
组成的方程组与 同解)
同解)
- 例2

由于 ,故第
,故第 个方程是多余的。
个方程是多余的。
- 例2
- 一般,
 m个方程n个未知数的线性方程组,系数
m个方程n个未知数的线性方程组,系数 是第
是第 个方程第
个方程第 个未知数的系数。
个未知数的系数。 (数域),此时解也在
(数域),此时解也在 中。
中。
- 数域:复数的子集
 对加、减、乘、除(分母不为0)封闭,称
对加、减、乘、除(分母不为0)封闭,称 为数域。如
为数域。如 ,
, ,
, 。
。
2. 矩阵的有关概念
- 上述方程组完全由表
 决定,
决定,
- 由
 行
行 列的数(
列的数( )组成的表,用圆括号(或方括号)限定,称为数域
)组成的表,用圆括号(或方括号)限定,称为数域 上一个
上一个 矩阵。
矩阵。 - 矩阵中各行称为向量(行向量),如
 是一个向量,可看作一行的矩阵。同样的,各列称为列向量。
是一个向量,可看作一行的矩阵。同样的,各列称为列向量。 - 0向量:
 。
。
- 由
- 矩阵的初等变换:
 必可由初等变换化为阶梯形矩阵,称为方程组的矩阵消元法
必可由初等变换化为阶梯形矩阵,称为方程组的矩阵消元法
- 交换两行
 乘某行
乘某行- 某行k倍加到另一行
3. 解线性方程组的矩阵消元法
- 考虑方程组
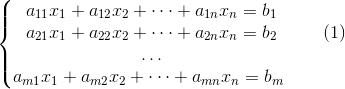
称 为
为 的系数矩阵,
的系数矩阵, 为
为 的增广矩阵。
的增广矩阵。
- 方程组
 与它的增广矩阵
与它的增广矩阵 互相唯一决定。
互相唯一决定。 - 对
 进行初等变换化为阶梯形,再解相应的阶梯形方程组。
进行初等变换化为阶梯形,再解相应的阶梯形方程组。 - 例

解: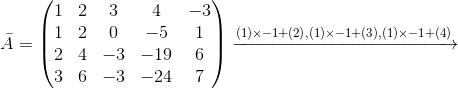

可见阶梯形可以不规则 改写为
改写为
令 自由取值为
自由取值为 ,得解
,得解
其中, 称为自由未知量,的原方程的无穷多组解。
称为自由未知量,的原方程的无穷多组解。 - 命题:设方程组的增广矩阵
 化为阶梯形后,含
化为阶梯形后,含 个非0行,且最后一个非0行
个非0行,且最后一个非0行 ,则方程组有
,则方程组有 个自由未知量,从而有无穷组解。(
个自由未知量,从而有无穷组解。( 称为矩阵
称为矩阵 的秩:化为阶梯形后的非0行数)
的秩:化为阶梯形后的非0行数) - 定理1:用初等行变换把增广矩阵
 化为阶梯形后,记
化为阶梯形后,记 为系数矩阵
为系数矩阵 的秩,
的秩, 为增广矩阵的秩(有
为增广矩阵的秩(有 ),则
),则
A. 时方程组无解
时方程组无解
此时最后一行 无解,表现为
无解,表现为 的阶梯形中最后一行为
的阶梯形中最后一行为
方程组有解
B. 时方程组有解
时方程组有解
a. (未知数个数),有无穷组解,此时有
(未知数个数),有无穷组解,此时有 个自由未知量
个自由未知量
b. 时有唯一一组解
时有唯一一组解
- 方程组
- 通解:设方程组有无穷组解
 ,则有
,则有 个自由未知量
个自由未知量 ,令
,令 得
得 其中
其中 称为方程组的通解。
称为方程组的通解。
通解也可写成向量式
- 特解:通解中的某个具体的解。
- 解集合:

4. 齐次线性方程组(右边常数项全为0)
这里只考虑一次齐次方程组
- 系数矩阵
 的秩
的秩 时必有非0解,
时必有非0解, 时只有0解
时只有0解 - 若齐次线性方程组的方程个数
 (未知数个数),必有非0解。(此时
(未知数个数),必有非0解。(此时 的必有非0解)
的必有非0解)
?
时间: 2024-12-23 19:07:38


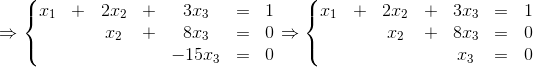

 是一些方程,称
是一些方程,称 为
为 组成的方程组与
组成的方程组与
 ,故第
,故第 个方程是多余的。
个方程是多余的。
 m个方程n个未知数的线性方程组,系数
m个方程n个未知数的线性方程组,系数 是第
是第 个方程第
个方程第 个未知数的系数。
个未知数的系数。 (数域),此时解也在
(数域),此时解也在 中。
中。 ,
, ,
, 。
。 决定,
决定,
 行
行 列的数(
列的数( )组成的表,用圆括号(或方括号)限定,称为数域
)组成的表,用圆括号(或方括号)限定,称为数域 矩阵。
矩阵。 是一个向量,可看作一行的矩阵。同样的,各列称为列向量。
是一个向量,可看作一行的矩阵。同样的,各列称为列向量。 。
。 乘某行
乘某行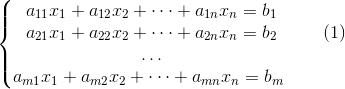
 为
为 的系数矩阵,
的系数矩阵, 为
为 互相唯一决定。
互相唯一决定。
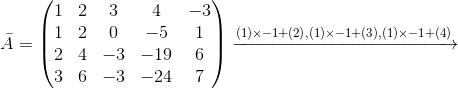

 改写为
改写为
 自由取值为
自由取值为 ,得解
,得解
 称为自由未知量,的原方程的无穷多组解。
称为自由未知量,的原方程的无穷多组解。 个非0行,且最后一个非0行
个非0行,且最后一个非0行 ,则方程组有
,则方程组有 个自由未知量,从而有无穷组解。(
个自由未知量,从而有无穷组解。( 称为矩阵
称为矩阵 为增广矩阵的秩(有
为增广矩阵的秩(有 ),则
),则 时方程组无解
时方程组无解 无解,表现为
无解,表现为

 时方程组有解
时方程组有解 (未知数个数),有无穷组解,此时有
(未知数个数),有无穷组解,此时有 时有唯一一组解
时有唯一一组解 ,令
,令 得
得 其中
其中 称为方程组的通解。
称为方程组的通解。

 时只有0解
时只有0解 (未知数个数),必有非0解。(此时
(未知数个数),必有非0解。(此时 的必有非0解)
的必有非0解)