## ~~话说这是博主的第一篇博客。。。~~
### 咳咳咳,今天讲的是DP的一种优化策略——矩阵乘法
关于能用矩阵乘法优化的DP题目,有如下几个要求:
1. 转移式只有加法,清零,减法etc.,max和min运算不允许
2. 转移式中关于前几位dp结果得到的系数必须是常量
3. 转移次数一般超级多
4. 由于转移次数多,一般都要模一个int范围内的数
综上,举一个例子:
> $dp[ i ]=a×dp[ i-1 ]+b×dp[ i-2]+c×dp[ i-3 ]$
其中,a,b,c是常量,而在需要矩阵优化的DP中,往往 i 在2^128之类的,特别鬼畜的特别大的数;
因为矩阵乘法优化后求dp[ i ] 是在O log(i)的时间内完成的。
那么,关于矩阵乘法如何实现,它的原理又是啥呢?
矩阵乘法需要两个矩阵A与B,A是n×p,B是p×m的大小,如下图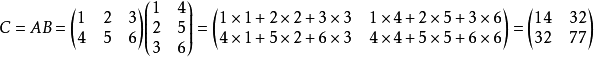
为了方便解释,我们举斐波那契的例子。
斐波那契的转移式是:dp[ i ]=dp[ i-1 ]+dp[ i-2 ]。
那么我们把(dp[ i ],dp[ i-1 ])看做一个1×2的矩阵A
而每次转移相当于把A乘以矩阵F:
|1 1|
|1 0|
得出的结果是:$(dp[ i ]+dp[ i-1],dp[ i ])$,也就是$(dp[ i+1 ],dp[ i ])$
那么每次进行一次矩阵乘法需要8次运算,而原先的状态转移只需要1次,这么看矩阵乘法不就一废柴算法吗。。
关键的是!矩阵乘法具有**结合律**, 嘿嘿嘿,那么我们就可以开始**快速幂**了!这样一下吧O(n)的朴素算法优化成了O(8×logn)的算法,在**n**炒鸡炒鸡变态大的时候我们就可以用这个优化了。
[斐波那契原题](https://www.luogu.org/problemnew/show/P1962)
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
long long n;
const int MOD=1e9+7;
void mul(int f[2],int a[2][2]){
int c[2];
memset(c,0,sizeof(c));
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
c[j]=(c[j]+(long long)f[k]*a[k][j])%MOD;
memcpy(f,c,sizeof(c));
}
void mulself(int a[2][2]){
int c[2][2];
memset(c,0,sizeof(c));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
c[i][j]=(c[i][j]+(long long)a[i][k]*a[k][j])%MOD;
memcpy(a,c,sizeof(c));
}
int main(){
scanf("%lld",&n);
int f[2]={0,1};
int a[2][2]={{0,1},{1,1}};
for(;n;n>>=1){
if(n&1) mul(f,a);
mulself(a);
}printf("%d\n",f[0]);
return 0;
}
```
斐波那契是二阶的矩阵乘法,复杂度为$O$(2^3^×logm),(m是需要DP到的序列的大小)还有三阶的甚至n阶的矩阵乘法,那样的话复杂度是$O$(n^3^×logm),关于三阶的例题:[三阶例题](https://www.luogu.org/problemnew/show/P1939)
三阶的话其实就把矩阵开成3×1和3×3的就可以了。
标程:
```cpp
#include<bits/stdc++.h>
using namespace std;
int T;
int n;
const int mod=1e9+7;
void mul(int f[3],int a[3][3]){
int c[3];
memset(c,0,sizeof(c));
for(int j=0;j<3;j++)
for(int k=0;k<3;k++)
c[j]=(c[j]+(long long)f[k]*a[k][j])%mod;
memcpy(f,c,sizeof(c));
}
void mulself(int a[3][3]){
int c[3][3];
memset(c,0,sizeof(c));
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
for(int k=0;k<3;k++)
c[i][j]=(c[i][j]+(long long)a[i][k]*a[k][j])%mod;
memcpy(a,c,sizeof(c));
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d",&n);
int f[3]={0,0,1};
int a[3][3]={{1,1,0},{0,0,1},{1,0,0}};
for(;n;n>>=1){
if(n&1) mul(f,a);
mulself(a);
}
printf("%d\n",f[0]);
}
return 0;
}
```
呃,在这里打个**广告**:[博主自己出的题,n阶的,差不多紫题吧](https://www.luogu.org/problemnew/show/T77626)
~~讲真超级水~~
### 接下来是比较经典的例题:
##### **例一**
设一个函数为f(n),表示从1到n所有整数连起来的数,例如:f(1)=1,f(6)=123456,f(11)=1234567891011。求f(n)模1e9+7的值
范围超大:n<=1e18
emmm,看的这道题,你发现就算是不模1e9+7把1e18这么多数直接输出都会爆炸,于是这题的算法就只能是O(logn)得啦QAQ。
于是我们发现f(n)可以由f(n-1)后面接上n得到,那么得出一个不可能计算的3×3转移矩阵:
| 10^log(n-1)^ 0 0|
|1 1 0|
|0 1 1|
而被乘矩阵为|f(n),n+1,1|
很明显,10^log(n-1)^是不可能算出来的,那么我们可以这样做:
例如n=999
|0 1 1| ×|10 0 0|^9^×|100 0 0|^90^×|1000 0 0|^899^
________|1 1 0| ___ |1 1 0| ______|1 1 0|
________|0 1 1| ___ |0 1 1| ______|1 1 0|
就解决啦啦啦啦(~ ̄▽ ̄)~
原文地址:https://www.cnblogs.com/china-xyc/p/11616820.html
