DES算法学习

密码学课程上老师讲DES很清楚，然而分成了几节课来讲总是断断续续的，理解的不够全面还容易忘记，因此这篇文章特地好好学习一些DES算法，并努力争取学习完后自己写出c程序。

本文内容大多翻译自J.Orlin Grabbe的The DES Algorithm Illustrated，外加一些自己的理解

背景

  1. 数据加密标准（Data Encryption Standard, DES）是一种对称密钥、块加密的加密算法
  • 1976年被美国联邦政府的国家标准局确定为联邦资料处理标准（FIPS），随后在国际上广泛流传开来
  • 它基于使用56位密钥的对称算法。
  • 这个算法因为包含一些机密设计元素，相对短的密钥长度（56位）以及怀疑内含美国国家安全局（NSA）的后门（sbox）而在开始时有争议，DES因此受到了强烈的学院派式的审查，并以此推动了现代的块密码及其密码分析的发展。
  • DES现在已经不是一种安全的加密方法，主要因为它使用的56位密钥过短。
  • 1999年1月，distributed.net与电子前哨基金会合作，在22小时15分钟内即公开破解了一个DES密钥。

    也有一些分析报告提出了该算法的理论上的弱点，虽然在实际中难以应用这些弱点。

  1. 为了提供实用所需的安全性，可以使用DES的派生算法3DES来进行加密，虽然3DES也存在理论上的攻击方法。
  • 在2001年，DES作为一个标准已经被高级加密标准（AES）所取代。另外，DES已经不再作为国家标准科技协会（前国家标准局）的一个标准。

准备工作

  • 关于二进制、十六进制、位等概念无需赘述
  • 需要说明的是DES算法，输入：64位明文；密钥：56位；输出：64位密文

实际上密钥也是64位的，但只使用其中的56位，并不使用8, 16, 24, 32, 40, 48, 56, 64这些位

加密过程

STEP 1

64位的key生成16个subkey，每个都是48位

1.使用PC-1表

使用方法：

  • K:原始密钥，K+：经过PC-1处理后的结果
  • PC-1是一个矩阵，对于每一项，值表示K的第几位，下标表示K+的第几位，比如，57表示“K的第57位成为K+的第1位”，49表示“K的第49位成为K+的第2位”
  • 例如：

    K=00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

    会得到

    注意我们忽略了8,16……64这些位，不让它们参与运算，所以K是64位，K+是56位

K+=1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111

2.拆分K+

  • 将K+拆分为左28位C0和右28位D0

如：K+=1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111，

则

  • C0 = 1111000 0110011 0010101 0101111

    - D0 = 0101010 1011001 1001111 0001111

3.生成块

  • 利用上面得到的C0和D0，来生成16个Dn和16个Cn（1<=n<=16）,Cn和Dn都分别从Cn-1和Dn-1得到
  • 方法是，将Cn-1（或Dn-1）循环左移1或2个位得到Cn（或Dn），具体是1还是2由n决定
  • 这张表说明了n和左移距离的关系
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
移位 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
  • 例如C2左移2个位得到C3，C15左移1个位得到C16
  • 此时我们得到了这样的结果
	C0 = 1111 0000 1100 1100 1010 1010 1111
	D0 = 0101 0101 0110 0110 0111 1000 1111
	C1 = 1110 0001 1001 1001 0101 0101 1111
	D1 = 1010 1010 1100 1100 1111 0001 1110
	C2 = 1100 0011 0011 0010 1010 1011 1111
	D2 = 0101 0101 1001 1001 1110 0011 1101
	C3 = 0000 1100 1100 1010 1010 1111 1111
	D3 = 0101 0110 0110 0111 1000 1111 0101
	C4 = 0011 0011 0010 1010 1011 1111 1100
	D4 = 0101 1001 1001 1110 0011 1101 0101
	C5 = 1100 1100 1010 1010 1111 1111 0000
	D5 = 0110 0110 0111 1000 1111 0101 0101
	C6 = 0011 0010 1010 1011 1111 1100 0011
	D6 = 1001 1001 1110 0011 1101 0101 0101
	C7 = 1100 1010 1010 1111 1111 0000 1100
	D7 = 0110 0111 1000 1111 0101 0101 0110
	C8 = 0010 1010 1011 1111 1100 0011 0011
	D8 = 1001 1110 0011 1101 0101 0101 1001
	C9 = 0101 0101 0111 1111 1000 0110 0110
	D9 = 0011 1100 0111 1010 1010 1011 0011
	C10 = 0101 0101 1111 1110 0001 1001 1001
	D10 = 1111 0001 1110 1010 1010 1100 1100
	C11 = 0101 0111 1111 1000 0110 0110 0101
	D11 = 1100 0111 1010 1010 1011 0011 0011
	C12 = 0101 1111 1110 0001 1001 1001 0101
	D12 = 0001 1110 1010 1010 1100 1100 1111
	C13 = 0111 1111 1000 0110 0110 0101 0101
	D13 = 0111 1010 1010 1011 0011 0011 1100
	C14 = 1111 1110 0001 1001 1001 0101 0101
	D14 = 1110 1010 1010 1100 1100 1111 0001
	C15 = 1111 1000 0110 0110 0101 0101 0111
	D15 = 1010 1010 1011 0011 0011 1100 0111
	C16 = 1111 0000 1100 1100 1010 1010 1111
	D16 = 0101 0101 0110 0110 0111 1000 1111

4.使用PC-2表

  • 使用结果： 56位的CnDn序列产生48位的Kn
  • 例如CnDn的第14位成为Kn的第1位，CnDn的第32位成为Kn的第48位
  • 此时我们得到
	K1 = 000110 110000 001011 101111 111111 000111 000001 110010
	K2 = 011110 011010 111011 011001 110110 111100 100111 100101
	K3 = 010101 011111 110010 001010 010000 101100 111110 011001
	K4 = 011100 101010 110111 010110 110110 110011 010100 011101
	K5 = 011111 001110 110000 000111 111010 110101 001110 101000
	K6 = 011000 111010 010100 111110 010100 000111 101100 101111
	K7 = 111011 001000 010010 110111 111101 100001 100010 111100
	K8 = 111101 111000 101000 111010 110000 010011 101111 111011
	K9 = 111000 001101 101111 101011 111011 011110 011110 000001
	K10 = 101100 011111 001101 000111 101110 100100 011001 001111
	K11 = 001000 010101 111111 010011 110111 101101 001110 000110
	K12 = 011101 010111 000111 110101 100101 000110 011111 101001
	K13 = 100101 111100 010111 010001 111110 101011 101001 000001
	K14 = 010111 110100 001110 110111 111100 101110 011100 111010
	K15 = 101111 111001 000110 001101 001111 010011 111100 001010
	K16 = 110010 110011 110110 001011 000011 100001 011111 110101

到这里我们终于得到了16个subkey

STEP 2

加密64位明文

1.使用IP表（Initial Permutation）

  • 使用结果：64位的明文M得到64位的IP
  • 例如，M的第58位成为IP的第1位，M的第7位成为IP的第64位
  • 此时我们得到

    M = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

    IP = 1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010

2.将IP分成左32位和右32位

  • 对于上面的IP我们得到

    L0 = 1100 1100 0000 0000 1100 1100 1111 1111

    R0 = 1111 0000 1010 1010 1111 0000 1010 1010

3.生成Ln和Rn

  • 对于上面得到的L0和R0，通过以下关系迭代得到Ln和Rn（1<=n<=16）

注意这里使用加号（+）来表示异或

  • 例如，n=1时

    K1 = 000110 110000 001011 101111 111111 000111 000001 110010

    L1 = R0 = 1111 0000 1010 1010 1111 0000 1010 1010

    R1 = L0 + f(R0,K1)

4.关于f函数

①使用E表(Expand)
  • 注意f的两个参数，Rn是32位，Kn是48位，因此我们需要对Rn进行扩展

  • 使用结果：32位的Rn成为48位的E(R0)
  • 使用方法同上，R0的第32位成为E(R0)的第1位，R0的第1位成为E(R0)的第48位
  • 此时我们得到

    R0 = 1111 0000 1010 1010 1111 0000 1010 1010

    E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101

②使用异或

  • 对于

    K1 = 000110 110000 001011 101111 111111 000111 000001 110010

    E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101

  • 我们得到

    K1+E(R0) = 011000 010001 011110 111010 100001 100110 010100 100111.

③使用S-box

注意f函数到现在还没有结束

  • 异或之后我们得到了48位的序列，6位一组将其分成8组，记为B1,B2,B3……B8
  • 对于每一个6位的Bi都要使用一次S-box，一共有8个box，B的下标和盒子的序号对应，即B1使用S1，B8使用S8
  • 使用结果6位的B产生4位的S，以S1为例

  • 使用方法：

    - B的第1位和最后一位组成的二进制数字表示box的行号（0011表示03）

    - B的中间4位组成的二进制数字表示box的列号（00001111表示016）

    • 这样6位的B会对应一个box中的数字，4个位
  • 例如，B：011011

    行号：01→1；列号：1101→13；查表得：5；转换成二进制：0101

    因此S1(011011)=0101

  • 具体的8个box可以查看文末的附录
④使用P表

注意到现在，f函数还是没有结束

  • 经过了8个box我们得到了S1S2……S8的32位序列

  • 使用结果：32位的S序列产生32位的f
  • 例如，S的第16位成为f的第1位，S的第25位成为f的第32位
  • 此时我们得到

    - S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)

    = 0101 1100 1000 0010 1011 0101 1001 0111

    - f = 0010 0011 0100 1010 1010 1001 1011 1011

⑤f函数的结束（终于结束啦）
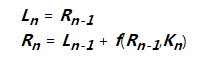
![](https://img2020.cnblogs.com/blog/1380694/202003/1380694-20200322150841918-1940103685.png)
  • 还记得这个公式吗？建议翻上去看看，绕得太多容易晕
  • 此时我们得到（注意加号表示异或）
    • R1 = L0 + f(R0 , K1 )

      = 1100 1100 0000 0000 1100 1100 1111 1111 + 0010 0011 0100 1010 1010 1001 1011 1011

      = 1110 1111 0100 1010 0110 0101 0100 0100

  • 注意前面的所有过程我们仅仅计算了R1，接下来使L2=R1，然后R2=L1+f(R1,K2)继续循环16次才能得到16个L和16个R

STEP 3

翻转序列LnRn成RnLn并查表

1.将经过f函数得到的序列LnRn翻转成RnLn，这两个序列都是64位

2.使用IP^(-1)表

  • 使用方法不再赘述
  • 例如

    - L16 = 0100 0011 0100 0010 0011 0010 0011 0100

    R16 = 0000 1010 0100 1100 1101 1001 1001 0101

  • 则

    - R16L16 = 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100

    - IP^(-1) = 10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101

3.到这里就已经大功告成了

  • 上面得到的IP^(-1)转换成16进制就是最后的密文
  • 整个DES加密结果是：

    M = 0123456789ABCDEF: C = 85E813540F0AB405.

总结

DES算法原理很简单，并没有什么不能理解的地方，让人望而生畏的是它那复杂的过程。需要注意的是查表的源-目标关系不要混乱。

　　接触了一些加密算法之后，总觉得所谓著名的加密算法就是过程怎么复杂怎么来，那些算法的发明者就是绞尽脑汁，逻辑位运算还不够，还得弄几个表来查查，等到最后自己都不知道绕了多少个弯、走到了哪一步、明文已经没人样的时候，这个伟大算法就算是成功了。无论如何致敬这些创造者吧！

原文地址：https://www.cnblogs.com/tc43/p/des_algorithm.html

时间： 2024-11-03 01:09:25

DES算法学习的相关文章

算法学习 - 表达树的建立（后缀表达式法），树的先序遍历，中序遍历，后序遍历

表达树就是根据后缀表达式来建立一个二叉树. 这个二叉树的每个叶子节点就是数,真祖先都是操作符. 通过栈来建立的,所以这里也会有很多栈的操作. 树的先序遍历,中序遍历,后序遍历的概念我就不讲了,不会的自行百度,不然也看不懂我的代码. 下面是代码: // // main.cpp // expressionTree // // Created by Alps on 14-7-29. // Copyright (c) 2014年 chen. All rights reserved. // #includ

我的算法学习之路

关于 严格来说,本文题目应该是我的数据结构和算法学习之路,但这个写法实在太绕口--况且CS中的算法往往暗指数据结构和算法(例如算法导论指的实际上是数据结构和算法导论),所以我认为本文题目是合理的. 这篇文章讲了什么? 我这些年学习数据结构和算法的总结. 一些不错的算法书籍和教程. 算法的重要性. 初学 第一次接触数据结构是在大二下学期的数据结构课程.然而这门课程并没有让我入门--当时自己正忙于倒卖各种MP3和耳机,对于这些课程根本就不屑一顾--反正最后考试划个重点也能过,于是这门整个计算机专业本

算法学习三阶段

?? 第一阶段:练经典经常使用算法,以下的每一个算法给我打上十到二十遍,同一时候自己精简代码, 由于太经常使用,所以要练到写时不用想,10-15分钟内打完,甚至关掉显示器都能够把程序打 出来. 1.最短路(Floyd.Dijstra,BellmanFord) 2.最小生成树(先写个prim,kruscal 要用并查集,不好写) 3.大数(高精度)加减乘除 4.二分查找. (代码可在五行以内) 5.叉乘.判线段相交.然后写个凸包. 6.BFS.DFS,同一时候熟练hash 表(要熟,要灵活,代码要

周总结(2017.2.16):第一周算法学习。

周总结:算法学习总结之DFS和BFS 一:DFS算法 目的:达到被搜索结构的叶节点. 定义:假定给定图G的初态是所有的定点都没有访问过,在G中任选一定点V为初始出发点,首先访问出发点并标记,然后依次从V出发搜索V的每个相邻点W,若W未曾出现过,则对W进行深度优先遍历(DFS),知道所有和V有路径相通的定点被访问. 如果从V0开始寻找一条长度为4的路径的话: 思路步骤: 先寻找V0的所有相邻点:dis{v1,v2,v3},V1没有访问过,所以对V1进行深度遍历并将V1标记为访问过,此时路径长度为1

算法学习 - 01背包问题（动态规划C++）

动态规划 01背包 问题描述 求解思路 代码实现 放入哪些物品 代码 动态规划 我在上一篇博客里已经讲了一点动态规划了,传送门:算法学习 - 动态规划(DP问题)(C++) 这里说一下,遇到动态规划应该如何去想,才能找到解决办法. 最主要的其实是要找状态转移的方程,例如上一篇博客里面,找的就是当前两条生产线的第i个station的最短时间和上一时刻的时间关系. minTime(station[1][i]) = minTime(station[1][i-1] + time[i], station[

LCA 算法学习 （最近公共祖先）poj 1330

poj1330 在求解最近公共祖先为问题上,用到的是Tarjan的思想,从根结点开始形成一棵深搜树,处理技巧就是在回溯到结点u的时候,u的子树已经遍历,这时候才把u结点放入合并集合中,这样u结点和所有u的子树中的结点的最近公共祖先就是u了,u和还未遍历的所有u的兄弟结点及子树中的最近公共祖先就是u的父亲结点.这样我们在对树深度遍历的时候就很自然的将树中的结点分成若干的集合,两个集合中的所属不同集合的任意一对顶点的公共祖先都是相同的,也就是说这两个集合的最近公共祖先只有一个.时间复杂度为O(n+q

算法学习 - 链表的游标实现~ C++

链表的游标实现,就是用另外一种方法来访问链表,模拟游标. 在我学习的理解中,就是创建一个节点数组,模拟内存的排列,然后从其中来申请内存和释放内存.但是实际的内存没有被释放~ 下面直接贴代码了: // // main.cpp // CursorList // // Created by Alps on 14-7-27. // Copyright (c) 2014年 chen. All rights reserved. // #include <iostream> #define CursorSp

最短路径算法学习总结

Dijkstra最短路径算法: dijkstra 算法的优点在于可以求出从一点到所有其他点的最短距离: input: 5 71 2 101 3 201 5 302 5 102 3 54 5 204 3 30 output: 0 10 15 40 20//这是求的在这颗树中,1到所有点的最短距离 1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 const int N=1100; 5 const int

Reinforcement Learning Q-learning 算法学习-2

在阅读了Q-learning 算法学习-1文章之后. 我分析了这个算法的本质. 算法本质个人分析. 1.算法的初始状态是随机的,所以每个初始状态都是随机的,所以每个初始状态出现的概率都一样的.如果训练的数量够多的 话,就每种路径都会走过.所以起始的Q(X,Y) 肯定是从目标的周围开始分散开来.也就是目标状态为中心的行为分数会最高. 如 Q(1,5)  Q(4,5)  Q(5,5)这样就可以得到第一级别的经验了.并且分数最高. Q(state, action) = R(state, action)