《A First Course in Probability》-chaper4-连续型随机变量-随机变量函数的期望

联系在离散型随机变量的引入过程，在定义了随机变量X的期望E[X]之后，我们在实际问题中往往还会关注关于X的函数的随机变量E[g(X)],继续类比讨论离散型随机变量函数的期望的结论，我们很容易进行如下的猜想：

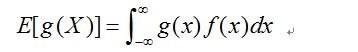
但是我们应该注意到，在离散型随机变量中，由于这种函数关系g(X)不会改变之后的概率分布，所以离散型随机变量的函数期望的求解公式在我们看来是显而易见的。但是在这里却有所不同，这种函数关系g(X)很显然会破坏原有的随机变量的密度函数，也就是说随机变量Y=g(X)的密度函数并不是f(x)，因此这里我们通过简单的代换，显然是不足以体现这个猜测的正确性的，因此我们需要更加有力的证明过程。

我们可以先通过一个题目来尝试求解E[g(X)]:

很明显我们这里看到对于随机变量Y的密度函数已经发生了改变，也和我们在上文的言论呼应了起来。

那么，到底该如何证明一开始我们给出的才行呢？