01背包剖析
问题引入
题目来源:ACwing:01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8

搜索代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1005;
int f[N][N], w[N] , v[N] , n , m;
// x 代表i件 物品
// y 代表当前最大容量
int dfs(int x,int y)
{
if(f[x][y] != -1)return f[x][y];
int ans = 0;
if(x == 0)return 0;
if(y >= w[x])
{
ans = max(dfs(x - 1, y) ,dfs(x - 1, y - w[x]) + v[x]);
}else ans = dfs(x - 1, y);
return f[x][y] = ans;
}
int main()
{
fill(f[0],f[0] + N * N , -1);
cin >> n >> m;
for(int i = 1; i <= n ;i ++)
{
cin >> w[i] >> v[i];
}
cout << dfs(n, m) << endl;
return 0;
}
虽然记忆化搜索的方式已经大大的优化了代码但是远远没有达到动态规划的\(O(VN)\)级别的复杂度
引入01背包问题的动态规划方式
和记忆化搜索一样我们依旧将问题分割考虑在背包容量为 j 的情况的下从前i个物品中能取得的最大价值
定义 : f[i][j] : 表示该状态
由于每件物品只有放和不放两种状态
放: f[i][j] = max(f[i-1][j],f[i-1][j-w[i]] + v[i])
不放:f[i-1][j] = f[i-1][j]
故根据以上状态转移方程我们可以得出下表
dp代码
#include <iostream>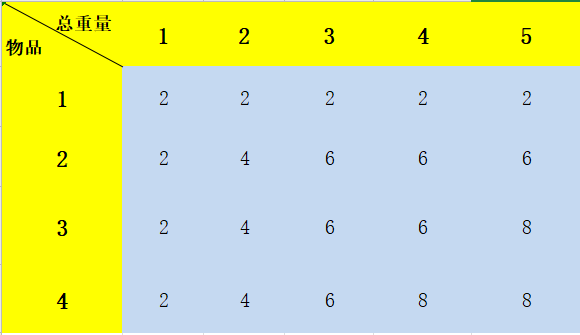
#include <algorithm>
#include <string>
using namespace std;
const int N = 1005;
int v[N],w[N],f[N][N];
int main()
{
int n , m;
cin >> n >> m;
for(int i = 1;i <= n;i ++)cin >> v[i] >> w[i];
for(int i = 1;i <= n;i ++)
{
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i])f[i][j] = max(f[i][j],f[i-1][j - v[i]] + w[i]);
}
}
cout << f[n][m];
return 0;
}
一维优化
通过观察我们可以发现我们的每一次的状态都仅由当前状态的前一层状态转移而来 故我们可以只保留上一层状态
来优化我们的存储空间 这种优化又叫做滚动数组
但是要注意更新状态的时候要采用倒序循环。
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
const int N = 1005;
int v[N],w[N],f[N];
int main()
{
int n , m;
cin >> n >> m;
for(int i = 1;i <= n;i ++)cin >> v[i] >> w[i];
for(int i = 1;i <= n;i ++)
{
for(int j = m; j >= v[i]; j--)
{
f[j] = max(f[j-1],f[j-w[i]] + v[i]);
}
}
cout << f[m];
return 0;
}
最长上升子序列问题(LIS)
问题描述:acwing895.最长上升子序列
\(O(n^{2})解法 动态规划\)
使用f[i]表示从第一个数字开始算,以w[i]结尾的最大的上升序列。(以w[i]结尾的所有上升序列中属性为最大值的那一个)
if(w[i] > w[j])
f[i] = max(f[i],f[j]+1);
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 10005;
int a[N] , f[N] , n ;
int main()
{
cin >> n;
for(int i = 1;i <= n ;i ++)scanf("%d",&a[i]);
int ans = 0;
f[0] = 0;
for(int i = 1; i <= n ;i ++)
{
f[i] = 1;
for(int j = 1;j < i;j ++)
{
if(a[i] > a[j])
{
f[i] = max(f[i],f[j] + 1);
}
}
ans = max(f[i],ans);
}
cout << ans << endl;
return 0;
}
原文地址:https://www.cnblogs.com/wlw-x/p/12636743.html
