数据结构 树的遍历（递归遍历）

//树的遍历--递归遍历
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

typedef struct _TreeNode{
    //数据域
    char data;
    //指针域
    struct _TreeNode * leftchild;//左孩子指针
    struct _TreeNode * rightchild;//右孩子指针
}TreeNode, *TreeNodePointer;

//先序遍历
 void PrintRoot(TreeNodePointer root){
    if (root!=NULL)
    {
        //访问根节点
        printf("%c", root->data);
        //访问左子树
        PrintRoot(root->leftchild);
        //访问右子树
        PrintRoot(root->rightchild);
    }
}

 //中序遍历
void PrintRoot2(TreeNodePointer root){
    if (root != NULL)
    {
        //访问左子树
        PrintRoot2(root->leftchild);
        //访问根节点
        printf("%c", root->data);
        //访问右子树
        PrintRoot2(root->rightchild);
    }
}

//后序遍历
void PrintRoot3(TreeNodePointer root){
    if (root != NULL)
    {
        //访问左子树
        PrintRoot3(root->leftchild);
        //访问右子树
        PrintRoot3(root->rightchild);
        //访问根节点
        printf("%c", root->data);
    }
}

void Test2(){
    //定义结构体对象
    TreeNodePointer t1 = NULL, t2 = NULL, t3 = NULL, t4 = NULL, t5 = NULL;
    t1 = (TreeNodePointer)malloc(sizeof(TreeNode));
    if (t1 == NULL)
    {
        printf("分配内存失败！");
        goto END;
    }
    //初始化数据
    memset(t1, 0, sizeof(TreeNode));
    t2 = (TreeNodePointer)malloc(sizeof(TreeNode));
    if (t2 == NULL)
    {
        printf("分配内存失败！");
        goto END;
    }
    //初始化数据
    memset(t2, 0, sizeof(TreeNode));
    t3 = (TreeNodePointer)malloc(sizeof(TreeNode));
    if (t3 == NULL)
    {
        printf("分配内存失败！");
        goto END;
    }
    //初始化数据
    memset(t3, 0, sizeof(TreeNode));
    t4 = (TreeNodePointer)malloc(sizeof(TreeNode));
    if (t4 == NULL)
    {
        printf("分配内存失败！");
        goto END;
    }
    //初始化数据
    memset(t4, 0, sizeof(TreeNode));
    t5 = (TreeNodePointer)malloc(sizeof(TreeNode));
    if (t5 == NULL)
    {
        printf("分配内存失败！");
        goto END;
    }
    //初始化数据
    memset(t5, 0, sizeof(TreeNode));
    //填充数据域
    t1->data = ‘A‘;
    t2->data = ‘B‘;
    t3->data = ‘C‘;
    t4->data = ‘D‘;
    t5->data = ‘E‘;

    //建立树之间的关系
    t1->leftchild = t2;
    t1->rightchild = t3;

    t2->leftchild = t4;
    t2->rightchild = NULL;

    t3->leftchild = t5;
    t3->rightchild = NULL;

    // t5是t4的左孩子
    t4->leftchild = NULL;
    t4->rightchild = NULL;

    //t5没有孩子节点
    t5->leftchild = NULL;
    t5->rightchild = NULL;

    //递归遍历树
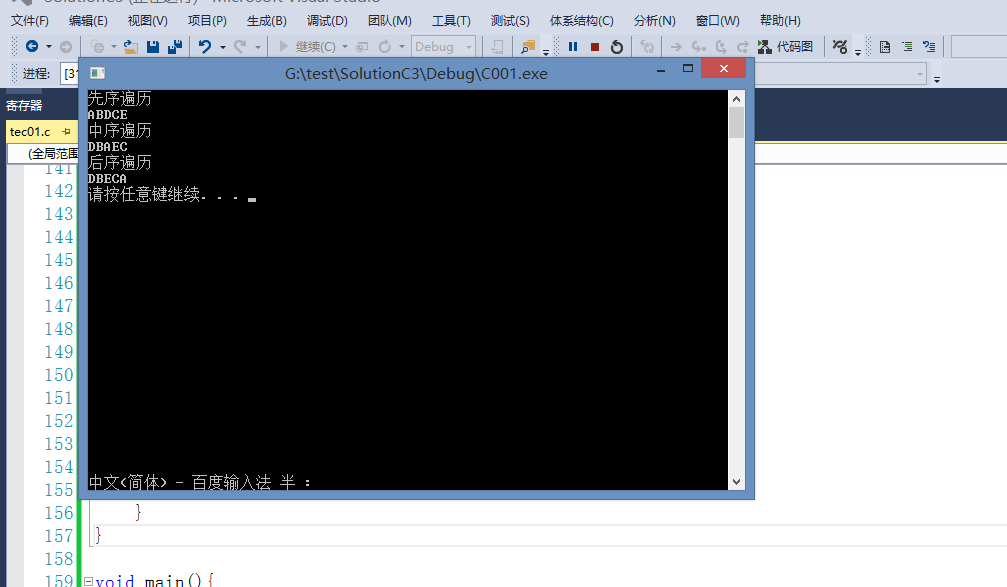
    printf("先序遍历\n");
    PrintRoot(t1);
    printf("\n");
    printf("中序遍历\n");
    PrintRoot2(t1);
    printf("\n");
    printf("后序遍历\n");
    PrintRoot3(t1);

END:
    if (t1 != NULL)
    {
        free(t1);
        t1 = NULL;
    }
    if (t2 != NULL)
    {
        free(t2);
        t2 = NULL;
    }
    if (t3 != NULL)
    {
        free(t3);
        t3 = NULL;
    }
    if (t4 != NULL)
    {
        free(t4);
        t4 = NULL;
    }
    if (t5 != NULL)
    {
        free(t5);
        t5 = NULL;
    }
}

void main(){
    Test2();
    printf("\n");
    system("pause");
}