hdu-5714 拍照(二分+树状数组)

题目链接：

拍照

Time Limit: 6000/3000 MS (Java/Others)   

 Memory Limit: 65536/65536 K (Java/Others)

Problem Description

小明在旅游的路上看到了一条美丽的河，河上有许多船只，有的船只向左航行，有的船只向右航行。小明希望拍下这一美丽的风景，并且把尽可能多的船只都完整地拍到一张照片中。

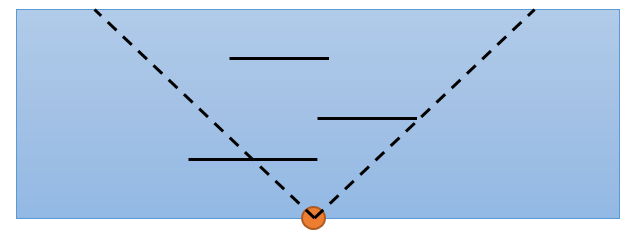
小明位于河的边上，并且可以在河边的任意位置进行拍照，照相机的视野恰好为90度角，只能以垂直于河边的方向进行拍照。河上的船只全都可看作是平行于河边的一条线段，跟河边的距离各不相同，有的正在向左移动，有的正在向右移动，但移动速度恰好都是一样的。小明可以等待恰当的时间让尽量多的船只都走进照相机的视野里，你不需要考虑船只之间会互相遮挡视野的情况。

![http://acm.hdu.edu.cn/data/images/C715-1003-1.jpg](http://acm.hdu.edu.cn/data/images/C715-1003-1.jpg)

Input

第一行为T，表示输入数据组数。

下面T组数据，对于每组数据：

第一行是一个数n(1≤n≤10^4)，表示船只的数量。

接下来n行，每行四个整数
x,y,z,d(−10^6≤x<y≤10^6,1≤z≤10^4)，表示船只的左端点位置、右端点位置、距离河边的距离，以及航行的方向。d为−1表示向左航行，1表示向右航行。

Output

对第i组数据，输出

Case #i:

然后输出一行，仅包含一个整数，表示最多可以拍到多少完整的船只。

Sample Input

3

2

1 3 1 1

2 4 1 -1

2

1 3 1 -1

2 4 1 1

1

1 4 1 1

Sample Output

Case #1:

2

Case #2:

1

Case #3:

0

题意：

思路：

[y-z,x+z]为岸上能看到这艘船的位置,这是一条线段,update(l,1)update(r+1,-1),然后就可以对于每一点可以query这点能看到的船的数量了;

范围太大,就可以把 这些线段离散化,只保留他们的端点,然后把这些端点的范围离散到[1,2*N]的范围内,大小的关系不变;

当然向左走和向右走的船要分开update,query;

最后得到答案后就要找最大值了,对于任意的一点,它能看到的最大的船的数目是这点后面所有点能看到的向左走的船的最大数目+这点之前所有点能看到的向右走的船的最大数目;

还有就是这个没必要用树状数组,可以直接最后扫一遍就可以得到每个点的能看到的船的数目了;

AC代码：

//#include <bits/stdc++.h>//有树状数组的
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<‘0‘||CH>‘9‘;F= CH==‘-‘,CH=getchar());
    for(num=0;CH>=‘0‘&&CH<=‘9‘;num=num*10+CH-‘0‘,CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + ‘0‘);
    putchar(‘\n‘);
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e4+15;

int n,sum[2][2*N],a[2*N],b[2*N],pre[2*N],nex[2*N];
int num,mmax;

struct node
{
    int l,r,d;
}po[2*N];

int findpos(int x)
{
    int l=1,r=mmax;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(b[mid]<x)l=mid+1;
        else r=mid-1;
    }
    return l;
}

int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int y,int flag)
{
    while(x<=mmax)
    {
        sum[flag][x]+=y;
        x+=lowbit(x);
    }
}
int query(int x,int flag)
{
    int s=0;
    while(x>0)
    {
        s+=sum[flag][x];
        x-=lowbit(x);
    }
    return s;
}

int main()
{
      int t;
      read(t);
      int Case=1;
      while(t--)
      {
          mst(sum,0);
          int x,y,z,d,cnt=1;
          num=0;
          mmax=0;

          read(n);
          Riep(n)
          {
              read(x),read(y),read(z),read(d);
              if(x+z<y-z)continue;
              po[cnt].l=y-z;
              po[cnt].r=x+z;
              if(d==-1)po[cnt++].d=0;
              else po[cnt++].d=d;
              a[++num]=y-z;
              a[++num]=x+z;
          }
          sort(a+1,a+num+1);
          b[++mmax]=a[1];
          for(int i=2;i<=num;i++)
          {
              if(a[i]!=a[i-1])b[++mmax]=a[i];
          }

          for(int i=1;i<cnt;i++)
          {
              po[i].l=findpos(po[i].l);
              po[i].r=findpos(po[i].r);
              update(po[i].l,1,po[i].d);
              update(po[i].r+1,-1,po[i].d);
          }
          for(int i=1;i<=mmax;i++)
          {
              pre[i]=max(query(i,1),pre[i-1]);
              nex[i]=query(i,0);
          }
          int ans=0;
          nex[mmax+1]=0;
          for(int i=mmax;i>0;i--)
          {
              nex[i]=max(nex[i+1],nex[i]);
              ans=max(ans,pre[i]+nex[i]);
          }
          printf("Case #%d:\n",Case++);
          print(ans);
      }
    return 0;
}
//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<‘0‘||CH>‘9‘;F= CH==‘-‘,CH=getchar());
    for(num=0;CH>=‘0‘&&CH<=‘9‘;num=num*10+CH-‘0‘,CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + ‘0‘);
    putchar(‘\n‘);
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e4+15;

int n,sum[2][2*N],a[2*N],b[2*N],pre[2*N],nex[2*N],sum1[2*N],sum2[2*N];
int num,mmax;

struct node
{
    int l,r,d;
}po[2*N];

int findpos(int x)
{
    int l=1,r=mmax;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(b[mid]<x)l=mid+1;
        else r=mid-1;
    }
    return l;
}

int main()
{
      int t;
      read(t);
      int Case=1;
      while(t--)
      {
          mst(sum,0);
          int x,y,z,d,cnt=1;
          num=0;
          mmax=0;

          read(n);
          Riep(n)
          {
              read(x),read(y),read(z),read(d);
              if(x+z<y-z)continue;
              po[cnt].l=y-z;
              po[cnt].r=x+z;
              if(d==-1)po[cnt++].d=0;
              else po[cnt++].d=d;
              a[++num]=y-z;
              a[++num]=x+z;
          }
          sort(a+1,a+num+1);
          b[++mmax]=a[1];
          for(int i=2;i<=num;i++)
          {
              if(a[i]!=a[i-1])b[++mmax]=a[i];
          }

          for(int i=1;i<cnt;i++)
          {
              po[i].l=findpos(po[i].l);
              po[i].r=findpos(po[i].r);
              sum[po[i].d][po[i].l]++;
              sum[po[i].d][po[i].r+1]--;
          }
          for(int i=1;i<=mmax;i++)
          {
              sum1[i]=sum1[i-1]+sum[0][i];
              sum2[i]=sum2[i-1]+sum[1][i];
              nex[i]=sum1[i];
              pre[i]=max(pre[i-1],sum2[i]);
          }
          int ans=0;
          nex[mmax+1]=0;
          for(int i=mmax;i>0;i--)
          {
              nex[i]=max(nex[i+1],nex[i]);
              ans=max(ans,pre[i]+nex[i]);
          }
          printf("Case #%d:\n",Case++);
          print(ans);
      }
    return 0;
}
时间： 2024-08-02 10:59:25

hdu-5714 拍照(二分+树状数组)的相关文章

HDU 1541 Stars （树状数组）

Problem Description Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given

HDU 3854 Glorious Array(树状数组)

题意:给一些结点,每个结点是黑色或白色,并有一个权值.定义两个结点之间的距离为两个结点之间结点的最小权值当两个结点异色时,否则距离为无穷大.给出两种操作,一种是将某个结点改变颜色,另一个操作是询问当前距离小于K的结点有多少对,K是一个定值. 思路:先求最初时候小于k的结点有多少对,然后每次改变颜色的时候,统计该点左侧和右侧各有多少同色和异色的结点(这一步使用树状数组),分别处理就行.另外需要预处理离某个结点最近的两个距离小于K的结点的位置. 代码写的略乱. #include<cstdio> #

HDU 3333 Turing Tree 树状数组 离线查询

题意: 给你一个数列,然后有n个查询,问你给定区间中不同数字的和是多少. 思路还是比较难想的,起码对于蒟蒻我来说. 将区间按照先右端点,后左端点从小到大排序之后,对于每个查询,我只要维护每个数字出现的最后一次就可以了(这个结论稍微想一下就可以证明是正确的). 然后就是简单的点更新,区间求和问题了- #include <cstdio> #include <cstring> #include <iostream> #include <map> #include

HDU 2689 Sort it (树状数组)

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2689 Sort it Problem Description You want to processe a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. Then how many times it 

HDU 2492 Ping pong (树状数组)

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2492 Ping pong Problem Description N(3<=N<=20000) ping pong players live along a west-east street(consider the street as a line segment). Each player has a unique skill rank. To improve their skill rank

11525 - Permutation（二分+树状数组）

题目链接:点击打开链接 题意:从1~k的所有排列中找到第n个排列, n由公式给出. 思路:可以发现, 这个公式就是康托展开公式(康托展开百科:点击打开链接). 那么s[i]的意思就是i个数中当前数排在第几. 如此, 可以用二分+树状数组快速求解, 和一道BC题目神似. 细节参见代码: #include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<st

Codeforces 374D Inna and Sequence 二分+树状数组

题目链接:点击打开链接 给定n个操作,m长的序列a 下面n个数 if(co>=0)则向字符串添加一个co (开始是空字符串) else 删除字符串中有a的下标的字符 直接在序列上搞,简单模拟 #include<stdio.h> #include<iostream> #include<string.h> #include<set> #include<vector> #include<map> #include<math.h&

【bzoj2527】[Poi2011]Meteors 整体二分+树状数组

题目描述 有N个成员国.现在它发现了一颗新的星球,这颗星球的轨道被分为M份(第M份和第1份相邻),第i份上有第Ai个国家的太空站. 这个星球经常会下陨石雨.BIU已经预测了接下来K场陨石雨的情况.BIU的第i个成员国希望能够收集Pi单位的陨石样本.你的任务是判断对于每个国家,它需要在第几次陨石雨之后,才能收集足够的陨石. 输入 第一行是两个数N,M. 第二行有M个数,第i个数Oi表示第i段轨道上有第Oi个国家的太空站. 第三行有N个数,第i个数Pi表示第i个国家希望收集的陨石数量. 第四行有一个

HDU 1541 Stars（树状数组）

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1541 解析: 题意:大概就是计算每颗星星左下边包括了多少颗星星,这个数值就是level.左下边不包括本身,不超过本身的x,y的坐标,可以等于.问每种level有多少颗星星. 这题,一开始想不到怎么用到树状数组,后来看了一下,发现题目给的数据是已经按x,y排好序的,所以我们可以不用管y的值. 注意: 1.每次输入一个坐标对之后,都要计算一下这个它的level. 2.此题的x坐标可以为0,而树状数组是从